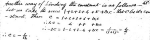Eins und eins zusammenzählen kann jeder. Zu eins wird noch eins hinzugefügt bzw. addiert (lateinisch addere). Dann wird gezählt und man erhält als Ergebnis die Summe zwei: 
. Wird zu eins zwei hinzugefügt, hat man als Ergebnis drei: 
. Wird zu eins und zwei drei hinzugefügt, gibt es sechs, usw. Was ist das Ergebnis der Addition aller natürlichen Zahlen? Ganz einfach: das Ergebnis ist minus ein Zwölftel,
![\[1+2+3+4+5+6+ \dots = -\frac{1}{12}!\]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-08b0015276783069c51abe11749ee1f6_l3.png "Rendered by QuickLaTeX.com")
Diese Erkenntnis verdanken wir dem indischen Mathemathiker Srivivasa Ramanujan [1]. Die Reihen
![\[ c= 1+2+3+4+5+6+ \dots\ \quad \mbox{und} \quad d=1-2+3-4+5-6+ \dots\]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-a9112d55c6fb40561ee2b707e71f5097_l3.png "Rendered by QuickLaTeX.com")
sind sich sehr ähnlich. Multipliziert man die Reihe 
mit 
und subtrahiert dann dieses Vierfache von der Reihe , d.h. 
, erhält man die Reihe 
![\[ d = c - 4\ c = 1+2+3+4+5+6+ \dots - (4 + 8 + 12 + 16 + 20 + 24 + \dots) = 1-2+3-4+5-6+ \dots \]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-7cbf4e03748b838eaf5b82c0685ba69d_l3.png "Rendered by QuickLaTeX.com")
Die Reihe
![\[ d = 1-2+3-4+5-6+\dots = \sum_{n=1}^\infty n\ (-1)^{n-1} \]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-7da2a2d00903604f7db33955e2cc966d_l3.png "Rendered by QuickLaTeX.com")
wiederum ist der Grenzwert der Reihe
![\[ \lim_{x \rightarrow 1}\sum_{n=1}^\infty n (-x)^{n-1} = \lim_{x \rightarrow 1}\frac{1}{(1+x)^2} = \frac{1}{4} \]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-ee33c08878c607c4733c9a1e66a7599d_l3.png "Rendered by QuickLaTeX.com")
Somit gilt 
und folglich
![\[ c = -\frac{1}{12}. \]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-ce9d628ce09a7446d99ef8348d84d881_l3.png "Rendered by QuickLaTeX.com")
Die Unendlichkeit trifft von hinten …..
Ebenso erstaunliche Ergebnisse wie die obige, divergente Reihe liefern die links unendlichen Zahlen. Reele Zahlen können unendlich viele Stellen hinter dem Komma aufweisen. Die dekadischen Zahlen haben unendlich viele Stellen vor dem Komma [2]. Für die dekadische Zahl 
gilt:
![\[\dots 999999 + 1 = \dots 00000000\ = e + 1 = 0\]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-4ea3e3696d76146a7f7fea6bb98c37d5_l3.png "Rendered by QuickLaTeX.com")
Daraus folgt 
bzw. 
. Die dekadische Zahl 
läßt sich als geometrische Reihe schreiben,
![\[\dots 111111 = \sum_{i=0}^\infty 10^i = \frac{1}{1-10} = -\frac{1}{9}.\]](https://alte-suedwand.at/wp-content/ql-cache/quicklatex.com-2a2c09e120adff31276febae2e9def20_l3.png "Rendered by QuickLaTeX.com")
Dieses Ergebnis hat durch den kanadischen Mathematiker Ilan Vardi eine besondere Anschauung erhalten. Ein Schütze wirft einen Pfleil. Der Pfeil fliegt zunächst sehr langsam, nur 1 Meter in 1 Sekunde. Aber dann beschleunigt er von Zauberhand: in der nächsten halben Sekunde fliegt er schon 10 Meter, in der darauffolgenden viertel Sekunde 100 Meter, usw. Voller Erstaunen macht er einen Schritt von 
Meter zurück und wird nach 2 Sekunden von seinem eigenen Pfleil durchbohrt.
Der Schütze, der seinen Pfeil in die Unendlichkeit geworfen hat, wird von hinten selbst getroffen ….
Quellen:
[1] Srinivasa Ramanujan, Notebook 1, Chapter 8, 1919
[2] Spektrum der Wissenschaft, Highlights 2/10, Seite 25 ff.
